Resumen física universitaria (Vectores)
- alejandrapanchanor
- 11 oct 2016
- 4 Min. de lectura
La física es una ciencia experimental y la más fundamental, por ende su estudio es muy importante. De tal manera que los científicos se apoyan en la teoría de la física. Esta ciencia contribuye con amplios beneficios y satisfacciones, estimula en la persona el pensamiento racional.
Magnitudes Escalares: Las cantidades escalares son números y se combinan con la aritmética usual.
Cuando una cantidad física se describe con un solo número, decimos que es una cantidad escalar. Las magnitudes escalares usan las operaciones aritméticas ordinarias. Por ejemplo, 6 kg +3 kg =.9 kg, o 4*2 s =8 s. No obstante, combinar vectores requiere un conjunto de operaciones diferente.
Algunas cantidades físicas, como tiempo, temperatura, masa y densidad se pueden describir completamente con un número y una unidad. No obstante, en física muchas otras cantidades importantes están asociadas con una dirección y no pueden describirse con un solo número. Un ejemplo sencillo es el movimiento de un avión: para describirlo plenamente, debemos indicar no sólo qué tan rápidamente se mueve, sino también hacia dónde.
Magnitudes vectoriales: Las cantidades vectoriales tienen tanto dirección como magnitud, y se combinan según las reglas de la suma vectorial.
El negativo de un vector tiene la misma magnitud pero apunta en la dirección opuesta.
Suma de vectores: Para entender mejor los vectores y su combinación, comencemos con la cantidad vectorial más sencilla, el desplazamiento, que es simplemente un cambio en la posición de un punto. (El punto podría representar una partícula o un cuerpo pequeño.) En la figura 1.9a representamos el cambio de posición del punto P1 al punto P2 con una línea que va de P1 a P2, con una punta de flecha en P2 para indicar la dirección.
El desplazamiento es una cantidad vectorial porque debemos decir no sólo cuánto se mueve la partícula, sino también hacia dónde.
Frecuentemente representamos una cantidad vectorial como el desplazamiento con una sola letra, como en la figura 1.9a. En este libro siempre simbolizaremos los vectores con letras negritas y cursivas con una flecha arriba, como recordatorio de que las cantidades vectoriales tienen propiedades diferentes que las cantidades escalares; la flecha nos recuerda que los vectores tienen dirección. Los símbolos manuscritos de los vectores suelen subrayarse o escribirse con una flecha arriba. Siempre escriba los símbolos vectoriales con una flecha arriba. Si no distingue entre cantidades vectoriales y escalares en su notación.
Observe que el desplazamiento no se relaciona directamente con la distancia total recorrida. Si la partícula siguiera a P2 y volviera a P1, el desplazamiento total sería cero (figura 1.9c).
Si dos vectores tienen la misma dirección, son paralelos; si tienen la misma magnitud y la misma dirección, son iguales, sea cual fuere su ubicación en el espacio.
Componentes de vectores
La suma vectorial puede efectuarse con componentes de vectores.
Para definir las componentes de un vector A partimos de un sistema rectangular de ejes de coordenadas y luego dibujamos el vector con su cola en O, el origen del sistema.

Podemos representar cualquier vector en el plano x, y como la suma de un vector paralelo al eje x y un vector paralelo al eje y. Rotulamos esos vectores como Ax en y Ay la figura 1.17a; son los vectores componentes del vector Ay su suma vectorial es igual a A simbólicamente.

La componente Ax de la suma vectorial es la suma de las componentes x de y en tanto que las componentes y y z se obtienen de forma análoga
Las componentes no son vectores Las componentes Ax y Ay de un vector son tan sólo números: no son vectores. Por ello, las simbolizamos con letra cursiva normal sin flecha arriba, en vez de la letra cursiva negrita con flecha que está reservadas para los vectores.
Podemos calcular las componentes del vector A si conocemos la magnitud A y su dirección
Cálculos de vectores usando componentes
Cálculo de la magnitud y la dirección de un vector a partir de sus componentes.
Podemos describir un vector plenamente dando su magnitud y dirección, o bien, sus componentes x y y. Las ecuaciones (1.6) indican cómo obtener las componentes si conocemos la magnitud y la dirección. También podemos invertir el proceso y obtener la magnitud y la dirección a partir de las componentes. Aplicando el teorema de Pitágoras a la figura 1.17b, vemos que la magnitud de un vector es:

La expresión para la dirección vectorial proviene de la definición de la tangente de un ángulo. Si medimos u desde el eje +x, y un ángulo positivo se mide hacia el eje +y entonces
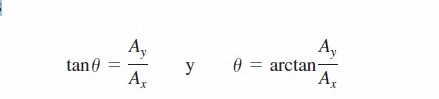
Siempre usaremos la notación arctan para la función tangente inversa
Multiplicación de un vector por un escalar. Si multiplicamos un vector por un escalar c, cada componente del producto es sólo el producto de c por la componente correspondiente de A
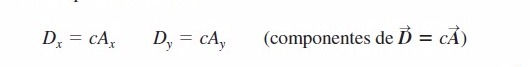
Vectores unitarios:
Los vectores unitarios describen direcciones en el espacio y tienen magnitud uno, sin unidades. Su única finalidad consiste en direccionar, es decir, describir una dirección en el espacio. Los vectores unitarios ofrecen una notación cómoda para muchas expresiones que incluyen componentes.
En un sistema de coordenadas x-y podemos definir un vector unitario i que apunte en la dirección del eje +x y un vector unitario j que apunte en la dirección del eje +y (figura 1.23a).

Así, expresamos la relación entre vectores componentes y componentes.
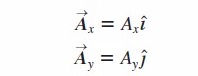
Producto de vectores
Hemos visto cómo la suma de vectores es consecuencia natural de combinar desplazamientos, y sumaremos muchas otras cantidades vectoriales posteriormente. También podemos expresar muchas relaciones físicas de forma concisa usando producto de vectores. Los vectores no son números ordinarios, así que no podemos aplicarles directamente la multiplicación ordinaria. Definiremos dos tipos diferentes de productos de vectores. El primero, llamado producto escalar, produce un resultado escalar.
El segundo, el producto vectorial, produce otro vector.
Producto escalar
El producto escalar de dos vectores A y B se denota con A*B Por esta notación, el producto escalar también se denomina producto punto. Aun cuando A y B sean vectores, la cantidad A*B es un escalar.
Para definir el producto escalar A*B dibujamos A y B con su cola en el mismo punto.












Comentarios